Range Voting versus other voting systems

These are the slides for WDS presentation to Colorado State legislature, 19 Sept. 2007.

Warren D. Smith (PhD)            Center for Range Voting    /    http://math.temple.edu/~wds/homepage/works.html

Plan/Goals

• Learn: What range voting is, what some other voting systems are, compare properties.
• If time, learn about "Bayesian Regret" and our computer simulations indicating objective sense RV better than all common voting system proposals
• Separate minitalk introduces "Proportional Representation" multiwinner voting systems
• These talk-slides will appear on web at /COlecture.html and the results of the mock election will be posted at /COsampleElection.html

Range Voting SAMPLE BALLOT

Range Voting ON A MACHINE or with OPSCAN BALLOTS

Award each candidate a numerical score from 0 to 9. Advise giving your favorite candidate 9 and the worst one 0. If you intentionally wish to express no opinion about that candidate, then leave the default "X" choice selected; only numerical scores will be incorporated into the averaging.

Also try zohopolls, or this instant runoff demo (IRV will not run on many of today's voting machines).

Simple fully-worked example of a small range-voting election

(The X's denote "intentionally left blank" by that voter to denote the fact he wishes to express ignorance/no opinion about Cal and wants to leave the decision about his score to other, more knowledgeable voters.)

Procedure: compute Amy's, Bob's, and Cal's sums, then compute their averages 32/4=8, 16/4=4, 15/3=5, Because Amy has highest average, she wins.

Who uses range voting?

• Olympics (To pick Gymnastics gold medalists, etc. since 1900) ⇒ highly familiar to all
• Internet sites like zohopolls.com, recipes, movie ratings, hotornot.com...
• Schools everywhere (to pick "valedictorians") – comparable number of these "elections" to all other kinds, so lots of successful experience (how often do you hear complaints about valedictorians gotten wrong, versus political elections?)
• But way before all that... honeybees have been range voting for millions of years in hundreds of trillions of "elections" (far more than all human-done elections)!

Range voting – only voting system endorsed by Mother Nature!

Top Single-Winner Voting Systems in one crib sheet

Are many other voting systems too... Also there are many Variant Rules for these systems...

Australia forces IRV voters to rank-order every candidate. Other places allow voters only to order some & omit others (automatically last-ranked). Some places force voters to rank their top K choices (for some fixed value K, such as 2 or 3) but no more. In range-voting, "no opinion" ("X") scores can also be permitted; these do not affect a candidate's average (then is common to refuse to permit somebody to win if he has too-few genuine, i.e. numerical, scores).

An Example

Plurality: A wins (most top-rank votes with 4).
Plurality+Runoff among top two: B wins over A in the runoff, 6-to-5.
Instant Runoff (IRV): C wins (eliminate E, D, F, and B in that order – doesn't matter which way you break DF tie – then C beats A in final round 7 to 4). IRV repeatedly deletes the candidate with fewest top-rank votes, then the remaining one wins.
Borda: D wins. (D's Borda score is 16+9+4+5+2=36 versus E with 12+12+6+1+3=34 and with lower scores for A, B, C, and F.) In the Borda system a candidate gets awarded 0 points if ranked last, 1 if ranked second-last, 2 if... and the candidate with the greatest score-sum ("Borda count") wins.
Condorcet: E wins. (Since E pairwise-beats each other candidate, e.g. beating A 6:5, B 6:5, C 7:4, D 6:5, and F 9:2.)
Approval Voting: If all the red candidates are "approved," then F wins with 7 approvals (versus A=4, B=5, C=3, D=6, E=5).

And with 0-99 Range Voting, it would in fact be possible to make any of the 6 candidates win, depending on how the voters chose the scores compatibly with the orderings above. In Range Voting each voter awards a score from 0 to 99 to each candidate; greatest average score wins. (Fancier rules allow also scoring a candidate with X = intentional blank = "no opinion" – only numerical scores incorporated into averages.)

Voter expressiveness

"Participation" property

Desirable property: A voter, by "participating" (i.e. casting an honest vote) should not worsen the election result from her point of view (versus if she had not voted).

Here A is eliminated in first IRV round, then B wins 10:8 over C. But if we add 3 more A>B>C voters, then B is eliminated in the first round, whereupon C wins 11:10 over A. By voting "C=worst," they made C win! These 3 voters would have been "better off staying home" and not voting.

How common is this problem? 16.2% in large 3-canddt IRV "random elections" (50% in those in which the IRV & plurality winners differ); if large number of candidates, conjecturally→100%.

"Favorite betrayal" and "spoilers"

Desirable property: A voter should be able to vote her favorite top, without fear that she will worsen the election result from her point of view (versus if she had dishonestly voted to pretend her favorite was below top).

This seems very important to make democracy work. If voting for your favorite is stupid, what kind of democracy is that?

This problem is common and called "spoiler." A Nader-top, Gore-second voter in Florida 2000, who voted honestly Nader-top, was being strategically unwise because her vote made her top & 2nd-choice candidates both lose. (Nader here was the "spoiler.") Lying in her vote (by voting Gore "top") would have been smarter; that way her 2nd favorite would win. Plurality voting system can reward voters who lie about their favorite. Side effect ("Duverger's law"): over time, kills off all "third parties."

Myth: IRV cures this problem. Reality: IRV still exhibits "spoilers," still encourages voters to lie about their favorite, and still kills off third-parties over time (Fiji; Australia where in all the state & federal IRV seats combined there is one third-party member).

In this 59-voter IRV election we've artificially named the candidates "Bush," "Gore" and "Nader" to remind you of FL 2000... (but are not claiming this resembles FL 2000 to more than a slight degree)

Under the rules of IRV, Gore is eliminated and the Gore second-votes go to Bush, who wins over Nader 30-29.

But what if 10 (or more) people in the third group, realizing Nader has no chance, strategically decide insincerely to lower Nader to 2nd or last place on their ballots? Then:

Now Bush and Gore get 20 first place votes apiece, and Bush only 19. Nader is eliminated first, giving 19 votes to Gore, and Gore crushingly beats Bush, 39-20. Those ten who switched their votes, got Gore (their second choice) instead of Bush (their third choice).

Betraying Nader paid off. IRV means betraying your true favorite third party candidate pays off. Voting third party can mean wasting your vote under IRV, just like under plurality.

How common is this problem? 19.6% in large 3-canddt IRV "random elections" but arguably 100% of the time if voters have "incomplete information" – i.e. very common.

Monotonicity

Desirable property: A voter, by increasing her vote for somebody, should not cause them to lose. (And decreasing your vote for somebody, should not cause them to win!)

Here IRV voting maximally against your favorite candidate – lying about everything & apparently the stupidest most-suicidal possible vote – makes your favorite win!!

How common is this problem? ≥4.9+12.2=17.7% in large 3-canddt IRV "random elections" (two kinds). (Can you say "lawsuit"?)

Immune to "candidate-cloning"

Desirable property: If new candidates that are almost exactly the same (in the view of every voter) as an old candidate X enter (or withdraw from) the race, that should not affect the winner (except for possible replacement by a clone).

Very serious problem because elections can easily be totally manipulated by, e.g. supporting candidates similar to your opponent to make both lose! Borda has opposite cloning problem ("teaming") – by running lots of clones of yourself, you (or a clone) win! (Battle of the clone armies!) Without clone-immunity, it is not about who is the best. It is about which party can summon up the most gall to try this nonsense.

Removing an "irrelevant loser" Candidate

4 candidates and 7 voters. Start looking at situation on left.

Finish order reverses with Borda!

Range, Approval, Plurality: Removing a loser (from all ballots & the election) never changes finish order for others. But with IRV a huge-loser can enormously change things even if only 2 voters (e.g. the candidate & spouse only) rank him top. "IRV chaos" example with 2025 voters and 12 candidates:

With IRV, who wins? And who is a "huge loser"? And how is this election going to be a huge chad-counting, lawsuit-flinging election-administration nightmare?

"Extremists" versus "Centrists"

What is a 2D "issue space"? Just a 2-dimensional notion of how people view two political issues. For example, the "Nolan chart" (invented by the Libertarian Party) – although you could instead employ any other two issues to make your own kind of chart.

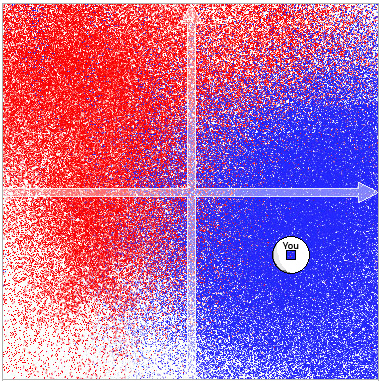
In below computer-generated pictures, voters prefer candidates closer to them. Each pixel is an ≈5000-voter election for a society that is a "bell curve" (in both directions) centered at that pixel. So each 200×200 picture exhibits 40,000 elections!

All voters vote honestly. Candidates are the little circles; pixel colors say which candidate won. The pictures in the top row are the hypothetical "optimum voting system," which always elects the best possible candidate for society (maximizing summed utility, utility being a decreasing function of voter-candidate distance). The corresponding pictures in the bottom row are IRV (Instant Runoff Voting).

Observations:

1. With IRV usually only about 7 of the 14 candidates can ever win. The other 7 are "zeroed out" and can never win, even when they are exactly located at the center of the voter distribution.
2. The 7 favored candidates are usually the 7 "extremists." The 7 "centrists" (located nearest the center of the picture) tend to be the ones IRV zeros out. The "extremist" win-regions grow into, invade, and take over "centrist territory."
3. IRV also exhibits some other strange phenomena. In several cases, a candidate has a disconnected win-region, for example the yellow region in the leftmost picture. (Why is that yellow "island" there in the middle of the olive-green "sea"? The yellow candidate is nowhere near. Surely the three candidates that actually are located on the island ought to win there? But no – IRV never permits any of them to win.) There are also several other "islands" and split win-regions in these pictures.
4. It turns out that every pixel where the IRV color disagrees with the Optimum color is an example of a situation in which IRV refuses to elect a "beats-all winner" who would defeat every opponent head-to-head. Some IRV-defenders have contended that such behavior is very rare. As you can see, that is not so; it can be quite common – happens for roughly 1/4 of the pixels in each IRV picture. You are looking at about 40,000 examples of this "very rare" behavior.
5. Why the "random dot" regions? "Tough call" near-tie elections...

Voting system	Favors Centrists or Extremists?
Plurality	Extremists
Approval	Centrists or no bias (depends on assumed voter "thresholding" behavior); also if they vote "plurality style" will duplicate plur's extremist-favortism
Condorcet Rank-order systems	no bias
Borda Rank-order; Range	little or no bias (pictures = slightly distorted version of above)
Instant Runoff (IRV)	Extremists

Countable in precincts?

Counting votes in precincts (or counties), then sending the precinct totals to the statewide election office – it has been a way of life in almost all US states for as long as any of us have lived.

But if we were to switch to IRV (instant runoff) voting, that would no longer be possible. All the votes, en masse, would have to be given to statewide central tabulating for them to count; there simply could no longer be such a thing as a "county subtotal."

This is not an insuperable obstacle to adopting IRV voting, but is a huge change in US election procedures, financing, and organization, and might make everything vulnerable to huge centrally-organized election frauds (can't observe your and your neighbors' own votes being counted anymore).

To make it clearer why there is no such thing as a district "subtotal" anymore if we use IRV voting, consider this 13+13-voter example:

So merging two districts both won by Bush under IRV, can produce an IRV victory for Gore.

What kind of voting machines can we use?

"Dumb totalizing" machines have their advantages. Cheap, simple, not computerized. But they were designed for Plurality voting. What if switch to some other voting system? Need to throw them in garbage? Do we need computerized machines (or a full-manual count)?

Auditability & Security Issues

How can you "audit" an IRV election? If no such thing as a "precinct subtotal," then idea of selecting random precincts for recounts as a sanity-check & "estimator of systematic bias & fraud," (e.g. required in upcoming federal HR811 bill) has less meaning...

If forced to use computerized machines and central counting, then how do you know election wasn't HACKED?? Princeton investigation of Diebold AccuVote-TS Voting Machine ("2nd-most commonly used machine in USA, used by 10% of all voters") revealed:

• Door on it – lock can be picked in 10 seconds.
• Also open with cheap "hotel minibar key" you can order off internet. Same key opens every Accuvote-TS machine in the world.
• Also, Diebold web page helpfully exhibits picture of key, and somebody actually used that picture to make their own key, sent it to Princeton, and it worked!
• Give me 1 minute access to machine. Just once. I open door, insert & withdraw memory card & game over. I own all elections conducted by that county forever into the infinite future. Why?
  1. Machines are programmed by Diebold to copy my takeover program off card & run it, no questions asked, no "signature" required, no encryption, no authorization check, nothing.
  2. From then on, whenever anybody uses a memory card (e.g. to transmit election data to central count) takeover program gets secretly copied on/off that card ("virus") and thus infects new machine.
  3. Machine acts normal for all voters and officials always... except... any later time, I walk into a polling place to cast my vote, and tap my magic musical sequence ("we are the champions"?) on it. Suddenly, an "enter your fraud" screen appears saying "who would you like to win, and by how much?" I tell it. Then more viral transmission, and election mysteriously comes out the way I want.
• Diebold also boasted their machines used "world class cryptography" to prevent unauthorized data transmission. Sounds great. Even the NSA cannot crack modern cryptosystems. Guessing the "secret key" is like guessing 200 coin flips in a row. Too many combinations. But...
• In 1997 Doug Jones (Iowa election examiner & CS professor) pointed out to Diebold that they appeared to be using the same secret key for every Diebold machine in the world. Completely nullifying security.
• Diebold ignored him.
• Diebold accidentally published this key on their internet site where anybody in the world could read it, along with their entire "secret" source code. It was analysed by Prof. Avi Rubin at Johns Hopkins University in 2003.
• After scandals came out about this & other horrible aspects of their engineering, Diebold claimed this was only for old software version. New versions are fine.
• That was a lie.
• As of 2007, Diebold machines with latest software (CA's Debra Bowen found when decertifying them) still doing this ten years later. Also, the "world class" cryptography was the DES system which had been broken, and the breaks published, in the mid-1990s.
• Not worried about Princeton hackers and NSA-like agencies? (You should be.) OK, top Diebold executives themselves include at least 5 convicted felons (drug dealing, 23 counts of theft, sophisticated computerized accounting fraud).
• How do you know they didn't hack the machines themselves? Diebold has many times illegally-installed "software updates" inspected by no-one; also Diebold accidentally published "private" ballot data they were not supposed to even have on their web site for all to see; also voting machine manufacturers have been involved in bribery scandals.

Moral

With IRV, computerized machines are not avoidable (unless go for full-manual count – not so easy for complicated system like IRV). Current computerized machines are hackable and fraudable and unbelievably poorly protected. These machines may well be declared illegal (California decertified all or most of them this year; San Francisco now apparently has to go to full-manual count). Then: big scandal and heavy expenses.

Range & Approval: don't need computer in your machine; don't need new machines or new software; easy to count. Easier transition.

Simplicity

Approval is the simplest system. Even simpler than plurality (no "overvoting=illegal" rule)! Note: the need to find and discard "overvotes," in plurality voting, causes many difficulties including machine- and fraud-related problems.

How can we measure "simplicity"?

• Size of computer program.
• Size of English description of rules.
• Voter reactions – how often do they produce invalid ballots?

Legislators can take something not-very-complicated, & complicate it

IRV and Condorcet are the most complicated commonly-proposed voting systems. But IRV doesn't seem that hard. (Pro-IRV propaganda calls it "Simple as 1-2-3.") Or is it? North Carolina adopted Instant Runoff Voting in a "pilot program" for use in 2007 and 2008 elections for local offices in volunteering jurisdictions.

VERBATIM rules description for IRV: as distributed to NC election officials. Note: hidden in there, these NC rules make several crucial changes to standard transferable-vote procedures (all for the worse in our view):

INSTANT RUNOFF VOTING in NORTH CAROLINA
2007 PILOT PROGRAM - M100 METHODOLOGY - VOTING

When the Instant Runoff Voting (IRV) method is used for a particular contest,
voting for one's top choice or choices is the same as if IRV were not used.
Each voter is allowed to vote for as many candidates as there are seats to be
filled in column A (see Exhibit I – Example IRV Ballot).

Each voter is then allowed the opportunity to indicate two alternate candidate choices, 
one per column in each of columns B and C, ranked in order of preference.

The voter has the option to choose alternate candidates.

For example, in the Office of Mayor contest there is one seat to be
filled. Each voter may vote for one candidate in column A, and then may indicate
a first alternate candidate choice in column B, and a second alternate candidate
choice in column C. In the City Council contest there are four seats to be filled. 
Each voter may vote for as many as four candidates in column A, and then may
indicate a first alternate candidate choice in column B, and a second
alternate candidate choice in column C.

COUNTING - FIRST ROUND
Only column A will be considered in the first round of counting.
If a voter overvotes in column A, no votes in that contest on that ballot will be
considered.  A voter may undervote in column A.
In the first round of counting, all ballots will be counted exactly
as if IRV were not used, with the exception that any results from columns B and C 
will be ignored.
If a sufficient number of candidates receive total votes exceeding the threshold of
victory for all seats in that contest to be filled, normal procedures apply
and there will be no need for a second round of counting. If all the seats are not
filled, those candidates which have won seats will be removed from further
consideration, and a number of candidates not exceeding twice the
number of remaining seats to be filled will advance to the second round of
counting, those candidates being the ones with the greatest numbers of first round
votes.

COUNTING - SECOND ROUND
If a second round of counting is required, the counting shall be
performed according to the following procedures:

A) Counting a single-seat contest:
1) Ballots shall be maintained in separate groups according to where or
how they were cast, by precinct or one-stop polling locations, or by
mail.
2) For each such group, ballots shall be separated into four stacks,
designated Stack A, Stack B, Stack C, and Stack O.
3) If a ballot was overvoted in column A, it shall be placed into
Stack O.
4) If a ballot contains a vote in column A for either runoff
candidate, it
shall be placed into Stack A. Because these votes have already been
counted in the first round, there is no need to count them again.
5) If a ballot does not contain a vote in column A for either runoff
candidate, but does contain a vote in column B for either runoff
candidate, it shall be placed into Stack B.
6) If a ballot does not contain a vote in either column A or B for
either runoff candidate, it shall be placed into Stack C.
7) Stack B ballots shall be counted by machine or by hand. Only those
votes cast for either runoff candidate in column B shall be considered.
These totals shall be added to the totals for those candidates from the
first round of counting.
8) Stack C ballots shall be counted by machine or by hand. Only those
votes cast for either runoff candidate in column C shall be considered.
These totals shall also be added to the totals for those candidates from
the first round of counting.
9) Repeat steps 1-8 as necessary until all ballots for the entire
jurisdiction have been counted.
10) The runoff candidate with the greatest total votes shall be
declared the winner.
B) Counting a multi-seat contest:
1) Ballots shall be maintained in separate groups according to where or
how they were cast, by precinct or one-stop polling locations, or by
mail.
2) For each such group, ballots shall be separated into five stacks,
designated Stack A, Stack B, Stack B2, Stack C, and Stack O.
3) If a ballot was overvoted in column A, it shall be placed into
Stack O.
4) If a ballot contains as many votes in column A as there are total
seats to be filled, and all such votes are for candidates who either won seats
in the first round or advanced to the second round, it shall be placed
into Stack A. Because these votes have already been counted in the
first round, there is no need to count them again.
5) If a ballot contains in column A exactly one undervote or exactly one
vote for a candidate who did not win a seat in the first round and did
not advance to the second round, and does contain a vote in column B
for any runoff candidate not already voted for in column A, it shall be
placed into Stack B.
6) If a ballot contains in column A more than one undervote or more than
one vote for candidates who did not win seats in the first round and did
not advance to the second round or at least one of each of these, and
does contain a vote in column B for any runoff candidate not already
voted for in column A, it shall be placed into Stack B2.
7) Of all remaining ballots, any which contains in column C a vote for a
runoff candidate already voted for in column A or B shall be placed into
Stack O, and the rest shall be placed into Stack C.
8) Stack B2 ballots shall be counted by machine or by hand. Only those
votes cast for a runoff candidate in column B shall be considered.
These totals shall be added to the totals for those candidates from the
first round of counting.
9) All Stack B2 ballots which contain in column C a vote for a runoff
candidate already voted for in column A or B shall be placed into Stack
O, and the rest shall be placed into Stack C.
10) Stack B ballots shall be counted by machine or by hand. Only those
votes cast for a runoff candidate in column B shall be considered.
These totals shall be added to the totals for those candidates from the
first round of counting.
11) Stack C ballots shall be counted by machine or by hand. Only those
votes cast for a runoff candidate in column C shall be considered.
These totals shall also be added to the totals for those candidates from
the first round of counting.
12) Repeat steps 1-11 as necessary until all ballots for the entire
jurisdiction have been counted.
13) The runoff candidate with the greatest total votes shall be
declared the winner of a seat in this contest.
14) If not all seats have been filled, for each precinct or other ballot
group recombine all ballots, then repeat steps 1-13 to determine the next
winner.

SUMMARY of voting system "Properties"

Voting system	Expressive	Participation	Favorite- Safe	Clone- Safe	Monotonic	Remove- Loser- Safe	Precinct- Countable	Dumb- Machines	Extremist/ Centrist Bias	Simplicity
Plurality	The Worst	yes	FAILS!	FAILS!	yes	FAILS!	yes	yes	Extremist	good
Approval	or on each canddt	yes	yes	partial	yes	yes	yes	yes	voter- behavior- dependent	best (excellent for meetings)
Condorcet systems	rank order	FAILS! (2.5%?)	FAILS!	yes & no	yes & no	FAILS! 9%	yes & no	FAILS!	unbiased	complex
Borda	rank order	yes	FAILS!	FAILS!	yes	FAILS!	yes	FAILS!	ok	medium
Instant Runoff (IRV)	rank order	FAILS! 16.2%	FAILS! 19.6-100%	yes	FAILS! 14.7%	FAILS!	FAILS!	FAILS!	Extremist	complex
Range	The Best	yes (if no "blanks")	yes	yes	yes	yes	yes	surprisingly yes	ok (bias, if any, small)	surprisingly good

How "honest" versus how "strategic" are voters?

• Plurality: about 90% of voters with Nader or Buchanan favorite (in USA 2000) actually voted for somebody else. Huge strategic dishonesty. (Devastates USA "third parties." Massive 2-party domination in USA: 99.5%.)
• IRV: less clear at present, but every IRV-using country has developed massive 2-party domination in all IRV seats. ("Spoiler effect" still happens, remember.)
• Range voting: surprise! A lot of voter "honesty" and non-strategy. Only about 25% of range voters vote in maximally-strategic, maximally-exaggerating-for-punch, "approval style" (all 9s and 0s, no intermediate scores). [See: USA range voting study (paper #82), French RV study or our TX governor race exit study]

Good. More voter honesty ⇒ better, less-strategically-distorted election results for all. But why happens?

• Psychological reasons – Range gives them more expressiveness and ability to be honest, and they don't want to waste that?
• Experiment on yourself! Do you want to give every candidate 9 or 0? You really don't want to, do you?
• Some strategic imperatives motivate more than others. Voters say "why should I dishonestly say the Socialist gets a zero, when honestly I feel he deserves 3 out of 9?" Socialist has no chance anyway, many voters aren't so worried they feel they need to lie to kill him off. Non-strong motivation to be strategically dishonest. Hence a lot of useful honesty will happen.
• Result (in our range voting USA exit poll in 2004): hugely more votes for third-party contenders relative to Bush & Kerry (but they still lost)

Our exit-poll (2004 Pres. election) Range and Approval study

Pseudo-election with real US voters (122 range & 656 approval) simultaneously with the 2004 presidential election (as exit poll). Note RV psychological drive for human honesty ⇒ hugely different election results – check out how hugely distorted our "democracy" is...

French 2007 study found different winner (the "centrist" Bayrou) from Range (also B. was a "beats-all" winner according to polls) than with their plurality+runoff 2nd round system (the "rightist" Sarkozy)

And in the 1980 US Presidential Election, according to analysis based on many polls in ch. 9 of Brams & Fishburn's book,

1992 results:

Candidate	Plur	AV
Clinton(Dem)	43.0	55
Bush(Rep)	37.4	49
Perot	18.9	42

Anderson probably actually would have come in second behind Reagan but ahead of Carter, under approval voting, whereas under plurality voting he was far in third place with under 7% of the votes. Again illustrates the tremendous distortionary penalty faced by third-party candidates under the undemocratic plurality system.

Importance of CASH as opposed to QUALITY

August 2007. Ames, Iowa. Romney overwhelmingly wins GOP straw poll. (Results delayed due to malfunctioning Diebold voting machines.) Romney spent $1 million on TV ads and to bus thousands of his supporters to Ames (many-hour bus rides, free wining & dining) and pay "poll tax" fees so they could vote for him in this poll! Far-outspent all rivals.

Why pay $1 million to fakely-win a straw poll??? Senseless? Unfortunately, is method to this madness.

• Plurality voting ⇒ strange dynamics.
• Voters strategically foolish to vote for anybody not in top two. (Otherwise your vote "wasted.")
• So you have to convince voters you are in the top two.
• Not about convincing them you are the best. About convincing them you are leading. That takes CASH.
• Politicians call this "momentum."
• Then voters "strategically forced" to vote for you and donors "forced" to give $ to you. (Like it or not.)
• So by creating a fake-lead in Iowa, Romney could well actually get a real lead (or real 2nd-place) in Iowa; that in turn gives him "momentum" in the USA as a whole!

BUT politics would be HEALTHIER if it were not about cash, not about constructing PR-illusions, not about "momentum" and trying to force voters to vote for you even though they dislike you – and more about actual candidate-quality. (You can be good quality choice without $millions.)

With favorite-safe systems like Range Voting, voter not "strategically forced" to vote against her true favorite when others lead in polls. Cash and faking leads are less important and quality is more important.

Primaries

Republican Party would also be healthier. Suppose Romney is poor-quality but manages to win the GOP nomination via such manipulations (made possible by plurality voting system in primaries and in straw polls). Then the entire GOP has been hurt and likely to lose presidency to a Democrat. Suppose GOP instead were to use range voting in primary and straw polls. Then would tend to nominate higher-quality candidates. That helps entire GOP and gives them better chances against the Democrat nominee (especially if the Dems foolishly do not use range voting in their primaries, hence they nominate low-quality choice).

(And could make the same argument about Hillary Clinton from the Dems' perspective...)

D & R parties – listen up! Our computer sims ⇒ you will gain ≈30-60% better chances to win the presidency if your party switches to range voting primaries!

Iowa 2008. 10 Rs, 10 Ds competing. Plurality system: voters "strategically forced" to vote for one of the "leading 2" even if not their favorite; we get the best-of-two. (E.g. Hillary Clinton probably one of the two. Even if 65% of Dem voters want non-Hillary, HC could still easily win Dem nomination due to anti-HC vote-split, etc.) Range voting: more like we get best of all 10. Which yields better result for the USA (and for your party's chances in the later general election)?

Because expect 10 Dem & 10 Repub candidates in primaries, range voting will have maximized quality advantage versus plurality & approval. Computer sims:

"Random normal elections": How often do the range & plurality winners agree?

#candidates:	C=2	3	4	5	8	10	15	20	50	100	200
5123 voters	100%	73%	61%	52%	38%	32%	24%	19%	8%	4%	2%

Approval versus Range

Best to regard Range & Approval not as rivals but rather as related / same thing (Approval=Range1).

Natural progression: Plurality → "Count All the Votes" = Approval → Range (What happens with Range? *Fractional votes are allowed.)

Legislation could adopt Approval in situations where speed and simplicity paramount (votes in meetings, or on stone-age voting machines) but with an upgrade to range9 or range99 mandated for future. As a stopgap, both could simultaneously be used (make Approval & Range9 & Range99 compatible by multiplying by 99 & 11 & 1).

Backsliding

Historically, many places & organizations that have adopted IRV have often decided to return to plain plurality voting. (Approximately same number of switches Plur→IRV as IRV→Plur.) Famous IRV→Plur Examples: New York City, Cincinnati.

Disquietingly, the IEEE abandoned Approval voting to backslide to plurality, and Dartmouth College may be about to do same, although there still are many more historical instances of Plur→Approval switch, than other direction.

But we are unaware of any organization that, once it had range voting, switched away from it.

How to evaluate/compare voting systems & seek best – 4 ways

0. Compare "properties" (as we've been doing)

Pros: Educational. Cons: which properties matter and how much, is subjective and eternally debatable; also just because a method fails some property logically, tells you nothing about how frequent and how serious that property-failure is in practice.

1. Look at human elections through history, or artificial ones (paid subjects).

Pros: Real; right sample space.
Cons[Historical]: Often hard to assess how "good" different election results were or would have been and what results "would" have occurred had other election method X had been used instead. (And subjective. And you'll be accused of bias.) Also, still not really correct sample space (since space might change over time with new X...).
Cons[Paid subjects]: Very expensive. Not really real.
Cons[Both]: Little data ⇒ low statistical significance ⇒ few results. And people lie to pollsters.

2. Has Darwinian Evolution (or "Intelligent design") made any animals that vote as important part of their life-cycle?

Yes! Already been done at least twice (social insects)!! Hundreds of trillions of very-important-to-the-insects elections so far! All voting systems considered (in some sense). Real (arguably more real than with humans - more years, more important to lives). Lots of data ⇒ high significance.

3. Measure "Bayesian regret" of different election methods via computer election simulations.

Pros: Large amounts of data ⇒ statistical significance is no problem. Artificial cyber-voters better than humans: Can read their "minds" to find their true desires unpolluted by lies (measured in standard "happiness units" too).
Cons: Computer results out = only as good as the assumptions & models in. Only try voting systems you try, not all possible.
Pros: Can try large number of assumption sets & models. If so lucky that in all of them, one voting method robustly is best, convincing.
Con: If not so lucky – some methods best in this model, others best in that ⇒ bummer.

What is Bayesian Regret?

Oversimplified into nutshell: "Bayesian regret" of election method E is "expected avoidable human unhappiness" caused by using E. Can be measured with computer simulations.

More precise answer: Bayesian regret is gotten via this procedure:

1. Each voter has a personal "utility" value for the election of each candidate. (E.g., if Nixon is elected, then Jill Voter acquires -55 extra lifetime happiness units.) In computer simulation, "voters" & "candidates" are artificial, and the utility numbers are generated by some randomized "utility generator" and assigned artificially to each candidate-voter pair.
2. Now the voters vote, based both on their private utility values, and (if strategic voters) on their perception from "pre-election polls" (also generated artificially within the simulation, e.g. from a random subsample of "people") of how the other voters are going to act.
   (Note. Some people here have gotten the wrong impression that this is assuming that voters will be "honest" or that we are assuming that honest range voters will use candidate-utilities as their candidate-scores. Neither impression is correct: These assumptions are not made.)
3. Election system E elects some winning candidate W.
4. The sum over all voters V of their utility for W, is the "achieved societal utility."
5. The sum over all voters V of their utility for X, maximized over all candidates X, is the "optimum societal utility" which would have been achieved if the election system had magically chosen the societally best candidate.
6. The difference between 5 and 4 is the "Bayesian Regret" of the election system E, at least in this experiment. It might be zero, but if E was bad or if this election was unlucky for E, then it will be positive because W and X will be different candidates.

Redo steps 1-6 zillion times (i.e. do zillion simulated elections) to find average Bayesian regret of election system E.

Comments: The Bayesian regret of an election system E may differ if we

1. Vary the number of voters,
2. Vary the number of candidates,
3. Vary the kind of "utility generator" (e.g. could be based on different numbers of "issues" with different methods for generating the locations of the candidates in "issue space"),
4. Use different kinds of assumed "voter strategy", or
5. Put different amounts of "voter ignorance". (*)

∃ at least 5 different "knobs" to "turn" on our machine for measuring Bayesian Regret of elctn method E.

Results of 1999 computer simulation study:

Measured Bayesian regrets for about 30 different election methods. 720 different "knob setting" combinations tried. Amazing result: in all 720 scenarios, range voting was best (had lowest Bayesian regret, up to statistically insignificant noise). We repeat: RV best in every single one of those 720 with either honest or strategic voters, regardless of ignorance-level, #candidates (3-5), #voters (5-200), #issues (0-∞) etc. [But no system, including range is "perfect"; all on average fall short of optimum utility.]

Typical BR results table (highly abbreviated)

Warning: Table makes it appear Borda is second-best after range. But in fact the full study considers hundreds of tables like this, & in many of them, Borda is not second best, in fact in many it's way down in the rankings. The question of which system is second best has no clear answer – some better in some kinds of election situations, others in others.

Moral:
Range voting will improve humanity's lot by about the same amount we got by inventing democracy. (And that, is big.)

Introduction to "proportional representation" multiwinner systems

If 51% Democrat voters, you could easily get 100% Democrat winners. (Massachusetts.) 51% Women voters, but way less than 51% women in the Senate. 12% Black voters, but way fewer in Senate. Only one atheist ever served in congress (or so they claim). Etc.

This is disproportionality. Many people feel it would be better if representatives were more... representative. For a voting system to offer any guarantee of that, it needs to be for multiwinner elections, e.g. 17-candidate, 5-winner elections.

Many naive ways to turn single-winner methods into multiwinner ones (e.g. "multiwinner plurality" where the top-W finishers win the W seats and you are granted W plurality votes) can totally fail to deliver proportional results. North Carolina's IRV-variant for multiwinner elections should tend to deliver 100% Democrat (or 100% Republican) winners, contrary to the professed aims of those behind that legislation.

"Hare/Droop reweighted STV" system (used in Ireland) is complicated. Involves rank-ordering votes, "reweighting" of votes so when X wins, then those who voted X now have their votes "deweighted" according to a magic formula, and then continue on to select next winner (then new reweighting) etc. Formula must be just right to get "proportionality theorem." Bizarre voter strategies (e.g. intentionally vote for no-hoper so your vote will retain high weight on an iffy seat; intentional vote-splitting in exactly the right proportions choreographed by parties distributing randomized "how to vote" cards) have been observed.

In "party list" systems (used in many countries, Germany, Israel, Netherlands) you do not vote for candidates, you vote for parties. A party with 27% of the votes gets 27% of the seats. But... that totally removes individual accountability and can have heavy biases based on party-size. (E.g. what if you aren't in a party?)

Harder to compare multiwinner systems ("Bayesian Regret" methodology only works for single-winner systems) and "properties" more complicated & less understood.

There is a provably-proportional multiwinner version of range voting called reweighted range voting

By act of Congress, multiwinner elections are currently illegal in the USA for Federal seats.

Proportional Representation versus Single-Winner / Summary

1. Single-winner voting systems "nonrepresentative" but aim to pick highest-quality winner. PR systems (involve multiwinner elections) sacrifice both perceived winner quality and accountability of politicians to voters, but seek to produce winners more "representative" of the electorate.
2. Range voting is single-winner and hence not PR. However, there is an alternate form of Range Voting designed for multiwinner elections and designed to exhibit proportionality, called reweighted range voting (RRV) – described in paper #78 at http://math.temple.edu/~wds/homepage/works.html.
3. PR federal elections are plausibly unconstitutional in the USA. If are constitutional, then conceivably PR could be achieved in the House of Representatives at least as far as the large states are concerned (but this probably would exacerbate power imbalance between large versus small states); but PR would be unachievable for Senate, US Presidency, and state governorships.
4. Which approach is better? Unclear philosophically, unclear based on historical evidence, and unclear based on economic statistical evidence. No consensus exists.
5. Therefore I am unsure PR is an improvement – but feel confident that switching from plurality voting to range voting is an improvement. (Much easier to understand and measure the relative quality of single-winner voting systems since can use Bayesian Regret, but no analogous quantity known for multiwinner systems.)
6. PR tends to get rid of 2-party domination. But not the only way to do that. The plurality + top-2-runoff(2nd round) single-winner system led in most or all of the large number of countries in which it has been tried, to having more than 2 important parties.
7. The very fact that neither PR nor non-PR (mainly plurality-voting-based) democracies exhibit obvious superiority over the other suggests that a democracy based on Range or Approval voting could be significantly superior to either (since good reason to believe it will be significantly superior to plurality-based majoritarian democracy).

Asset Voting – the simplest PR system (but untried)

There is one remarkably simple but unconventional kind of provably-proportional voting: Asset Voting. "Unconventional" because both the voters and the candidates participate. (Warning: this bothers a lot of people, and also prevents asset voting from being used at all in abstract scenarios with candidates that are not people, such as choosing pizza flavors.) Asset proven (in terms of certain criteria) superior to any "conventional" system.

Forest Simmons' simplified version of Asset voting to elect W winners from C candidates, 0 < W < C:

1. Each vote is "name one candidate" (plurality-style).
2. A candidate's "score" is the number of times he is named.
3. Now regard each score as the amount of an "asset" now owned by that candidate. The candidates now negotiate; any subset of them may redistribute their assets among themselves.
4. After all negotiations and redistributions end, the W "wealthiest" candidates win.

In variants, only certain kinds of redistributions are permitted, for example the candidates in increasing order of "wealth" drop out, redistributing their assets among the remaining ones as they do so. This "poorest first" variant has the advantage that it forces the procedure to end quickly and everybody knows when it has ended.

You can also compromise and, e.g, provide the voter with three plurality-style ballots, enabling her to split up her vote three ways – or fewer by using more than one ballot to vote for the same candidate.

Example

This is a make-believe analogue of the 2000 US presidential election. It's unrealistic in several ways, the most obvious being that it was a one-winner election, not a multiwinner election (asset voting can be used for single-winner elections but is intended for more-than-one-winner elections). Ignore the unreality. We are just trying to illustrate how it might work in a simple and familiar way.

In this election, Nader could decide to drop out of the picture and award his 20 asset points to Gore. (Both Bush and Gore would, no doubt, try to make deals with Nader to try to get his assets. But, let us suppose that Nader, after considering his options, the offered deals, and the fact he considered his views closer to Gore's than to Bush's, preferred Gore.) In that case, Gore would win with 37+20=57 asset points to Bush's 38. (Buchanan could also decide to give his assets to some candidate, but in the particular scenario here, Buchanan's decision would not be able to change the winner.)

Now if this were a 2-winner election, then both Bush and Gore would be winners no matter what Nader and Buchanan decided to do (albeit either Bush or Gore could in theory cause either Nader or Buchanan to be a winner by sacrificing their own chances – not likely).

Return to main RV page

Return to main page