By Forest Simmons Dec 2009.
Consider an election to determine which of four towns A,B,C,D should host the next harvest festival.
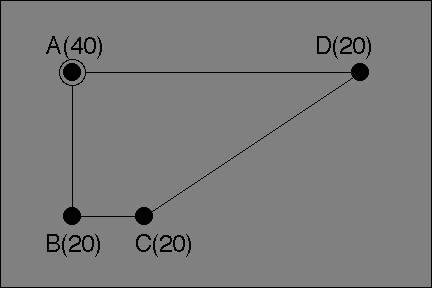
The respective town coordinates (in miles East and North of town B) and populations are:
| Town | Coordinates | Population | Euclidean Distances to A B C D |
"Taxicab" Distances to A B C D |
|---|---|---|---|---|
| A | (0, 2) | 40 | 0 2 √5 4 | 0 2 3 4 |
| B | (0, 0) | 20 | 2 0 1 √20 | 2 0 1 6 |
| C | (1, 0) | 20 | √5 1 0 √13 | 3 1 0 5 |
| D | (4, 2) | 20 | 4 √20 √13 0 | 4 6 5 0 |
Assuming voters prefer towns closer to them, the ballots are:
| #voters | Their Vote |
|---|---|
| 40 | A>B>C>D |
| 20 | B>C>A>D |
| 20 | C>B>A>D |
| 20 | D>C>A>B |
This makes D a "Condorcet loser" and creates the cycle A beats B beats C beats A, 60 to 40 in every case.
Remarks:
1.
Note that the
Poundstone example
has the candidate sites offset from the centers of support. It turns
out that this is inevitable in a three-candidate example, i.e.
if the respective supports are centered and
concentrated around the three respective candidates (and preferences respect distances)
then there can be no Condoret Cycle.
So my four-candidate geometrical example of a Condorcet cycle is minimal if you require the supporters to be concentrated around the candidate positions. (And divide our town populations by 20 to get really minimal about it.)
2.
This example has "wiggle room," i.e. the town distances,
coordinates, and
populations can be perturbed arbitrarily
without affecting our conclusions, as long as
the perturbations are not too large.
Note the example no longer works if "taxicab" (L1)
distances are employed instead of Euclidean (L2) distances.
However it will work with taxicab distances if, before we start, we
rotate the picture 44 degrees anticlockwise.
3. Personally I think it is pretty obvious A would be the best site. However, no voting method based purely on the pairwise preference counts – indeed, no method based purely on the 100 rank-orderings of the candidates by the voters – can possibly work to produce a preference for A over B or C. Only a voting method like range voting which also knows about strengths of preferences, could hope to do that.