(Skip to conclusion)
Rob Richie, the head of FairVote.org, on 8 May 2013, posted the following criticism of approval voting on the web as a comment to a video about approval voting. Richie's comment was directed to the judges of a contest and aimed to stop the video from winning that contest's multi-$1000 prize. We give Richie's entire criticism, verbatim, in full (no attempt to correct his spelling or grammar errors), with green background. We have numbered his paragraphs for reference.
1. Advocates of different methods of voting for single winner offices have a history of rather fractious behavior, but it's improving. Congratulations on that front to those seeking to work more cooperatively. 2. That said, here's the core difference of opinion. Aaron Hamlin is right that "you can always vote for your favorite in approval voting." That's a good thing, and a good reason to like the system. But problem is that voting for your second favorite can be a problem. Why? Because it counts equally with your favorite and, as a result, can lead to the defeat of your favorite candidate. That means anyone who think their favorite as a chance to win are going to be wary of voting for their second choice -- and we're heading back toward plurality voting dynamics. 3. Let's be concrete. Among the few examples of contested elections with approval voting are student elections for president the past couple years in Dartmouth. In both of them, the winner earned the approval of less than than 40% of voters. Perhaps that means voters just didn't know much about the candidates. But perhaps it means many didn't want to dilute their vote for their favorite by voting for their second favorite also. 4. Another example was at U-Colorado this year. In the two-candidate race for student government president, the result seems to have been 51.9% to 51.6%. The margin was 22 votes, with 246 students apparently voting for both candidates. Did those 246 students really mean to do that? Did they have a difference of opinion that might have tipped the balance if only voting for one ticket? 5. Ranked choice voting and traditional runoffs both don't have that property, which may explain why advocates of those approaches have been far more successful in having their reforms implemented and used in meaningfully contested elections. 6. But kudos for having a conversation about reform and it's great to focus on the fact that plurality voting is simply unacceptable -- as this video successful demonstrates. 7. Finally, let's keep in mind that if we want broader and fairer representation for more of us, we have to have more elections where more than one person wins -- and those winners can represent different opinions and voters. A big focus for some reformers is changing winner-take-all voting rules to fair voting plans like these ones FairVote has drawn for Congress at http://www.fairvoting.us |
In Richie's attempt to be "concrete" (his paragraphs 3 & 4) he actually cites five numbers in his entire criticism. We will now check his facts. We find that three of Richie's five numbers were wrong, for a total correctness rate of 40%. Congratulations Rob, you are, as you put it, "improving." And "kudos" to you for trying to mention facts. It would be better to actually cite sources for your facts because that tends to help in getting them right, and it would be better to aim for a correctness rate above 50%, since that way people would think you were more reliable than a random coin flip. But it's great to focus on having facts.
The University of Colorado. In the spring 2013 election for CUSG president, Lora Roberts, director of communications for CUSG, sent us the following in private email (in response to our enquiry): "The total number of voters was 6,686 in this election, which is the third largest in the last ten years." The election results were
| Chris Schaefbauer, Ellie Roberts, Marco Dorado, UNITE | 3354 (Elected) |
|---|---|
| Logan Schlutz, Alexis Scobie, Colby Schwartz, INSPIRE | 3332 |
Observe that 6686=3354+3332 exactly. Therefore, the total number of voters who voted for both candidates, was not 246, as Richie claimed, but exactly zero. (In order to have 246 both-way-voting voters, the total would have had to have been 6440=3354+3332-246 voters, in which case Richie's "51.6" and "51.9" still both would have been wrong.) The percentages were not 51.6 and 51.9, as Richie claimed, but 50.2 and 49.8. The correct figures show the exact opposite of what Richie was trying to show, in the most convincing manner possible (you cannot get lower than zero). But Richie did get the margin – 22 approvals – right: 3354-3332=22.
Dartmouth. As we will now show, Richie was correct that the winners in the 2 most recent student president elections did get <40% approval, although not the 3rd-most recent. (But I do not see why this represents something "wrong" with approval voting. If approval never permitted all candidates to have below 40% approval, which apparently is a situation Richie would prefer, then I would understand why that would be a distortionary voting system.):
In the election for 2013 Student Assembly president, Adrian Ferrari '14 was elected student body president with 736 approvals out of 1845 ballots cast (40% approval; on average each ballot approved 1.15 candidates), according to The Dartmouth 17 April 2013 article by Laura Weiss and another on 16 April by Michael Riordan:
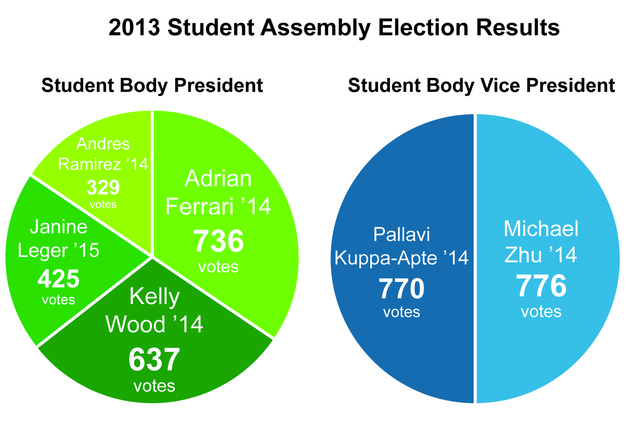
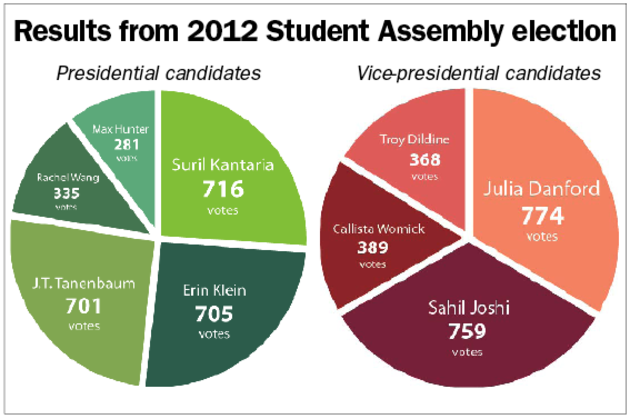
In the election for 2012 Student Assembly president, Suril Kantaria '13 was elected with 716 approvals feom 2239 voters (32% approval; on average each ballot approved 1.22 candidates) as explained in a 17 April 2012 article by Marina Shkuratov in the student newspaper The Dartmouth:
Finally, the election for 2011 student body president was won by Max Yoeli '12 with 691 approvals out of 1665 ballots (42%; on average each ballot approved 1.13 candidates) as reported in 18 April 2011 article by Marina Shkuratov in The Dartmouth. You can find out considerably more about this interesting 2011 election here.
More importantly than Dartmouth, all three of France's presidential elections of 2012, 2007, and 2002, were studied with an approval-voting-style exit poll study, and in them the winner had, respectively, 61%, 42.8%, and 36.7% approval, with the voters approving, on average, 2.58, 2.33, and 3.15 candidates. In the 2007 French election, incidentally, Approval worked well, electing the Condorcet winner Bayrou, while IRV malfunctioned, electing Sarkozy.
It is quite common that the winner has below 50% approval – but also quite common for him to have above 50%. For more examples, the "approval ratings" of US presidential candidates (in polls approaching election day) are given here. We find
| Winning Canddt | Year | Approval & DisApproval% |
|---|---|---|
| G.Bush I | 1988 | 49 & 41 |
| W.Clinton | 1992 | 41 & 42 |
| W.Clinton | 1996 | 46 & 37 |
| G.Bush II | 2000 | 58 & 36 |
| G.Bush II | 2004 | 53 & 46 |
| B.Obama | 2008 | 74 & 15 |
| B.Obama | 2012 | 53 & 45 |
It is however, quite rare that real world approval voters approve both of the top-two most likely candidates to win in situations where there are 2 main rivals and the rest have smaller chances. (The way Richie fantasized happened in CU's 2013 election.) It can certainly happen, but voters rarely are that strategically stupid. We have data on this. Thus in the 2002 France election, the two top approval rivals were Chirac & Jospin, no others came close enough to be likely to win. There were only 15 voters who approved both, out of 2597 total voters, i.e. 0.58%. Why did those 15 voters do this? We don't know, but possibilities include:
More interesting are races where there are three big rivals all with roughly equal chances. (E.g. Dartmouth's 2011 and 2012 races.) In that case, approving 1 or approving 2 of the three can be strategically wise, but it is unwise to approve 0 or 3. (Although, again, for a voter who does not care which of the three win, it would be reasonable to approve either none or all 3.)
Deceptive logic.
We also object to the following.
Richie deceptively
acts as though in "ranked choice voting"
there is no strategic reason not to rank your favorite first and
your second favorite second. That's wrong.
(Here "ranked choice voting" is the deceptive name Richie promulgated for
Instant Runoff Voting – IRV –
actually there are
Indeed, Although Richie complains that "[approving] your second favorite... can lead to the defeat of your favorite [with approval voting]" he fails to mention that voting for your genuine favorite can lead to his own defeat [with Richie's recommended system IRV]. Doesn't that seem more serious? Election example:
|
|
In the IRV election at left, A wins. (IRV eliminates C then A beats B by 17 to 12.) That is because 2 "B>C>A" voters foolishly voted for their favorite B. If they had instead lowered B in their rankings, dishonestly voting "C>B>A", then we'd instead have election at right. In that election B wins. (IRV eliminates A, then B beats C by 19 to 10.)
In fact, both "ranking your favorite top" and "ranking your second-favorite 2nd-top" can be strategic mistakes by an IRV voter which cause a worse candidate to win, than if that voter had lied about her favorite (or lied about her 2nd favorite, or lied about both, or refused to vote at all). In short, in Instant Runoff Voting it can be a strategic mistake to tell the truth about your favorite. It can also be a strategic mistake to tell the truth about your second-favorite. It can also be a strategic mistake to vote at all. Also IRV voters can be forced to dishonestly pretend their 2nd favorite is better than their true favorite. The ways in which these phenomena can happen can be surprising and unexpected, but unfortunately arise fairly frequently. Indeed, Rob Richie, in his only publication ever in a scientific journal, [with Terrill Bouricius & Philip J. Macklin in Science Magazine 294,5541 (May 2001) 303-306] stated "Used for decades in Australia and Ireland and considered in 13 state legislatures this year, IRV lets voters rank candidates in preference order. A voter's best strategy is to sincerely rank the candidates." This quote was simply false. It is not true that a voter's best strategy in IRV, is to sincerely rank the candidates. But kudos for Rob Richie for publishing in a scientific journal! It's just too bad that the most important claim in his article was false and was refuted by return mail – but he's trying so hard!
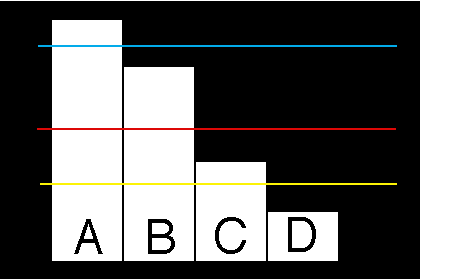
In contrast in approval voting, it is never a strategic mistake to truthfully approve your favorite. It can be a strategic mistake to approve your second-favorite (might defeat your favorite!), but probably more often, it is a strategic mistake to fail to approve your second-favorite. (You might get stuck with some winner you really hate, rather than your 2nd choice, who was decent.) But with approval voting, neither approving, nor disapproving, your 2nd-favorite, is "dishonest." Depending on the quality-level you choose for your "approval threshold" both could be regarded as "honest."
Pictorial example: If you use the blue line as your "approval threshold," then approve A only. If the red line, then approve both A and B. If the yellow line, then approve A,B, and C. All would be "honest" approval votes. (The vertical axis is "candidate quality" as perceived by some voter, namely you. Approving D but not A would be a "dishonest" approval ballot. We do not recommend that.)
You, the voter, have to make that strategic call to decide which risks are more probable and more severe – but either way you go, you still have not sunk to lying. And it is straightforward to make that call, unlike in IRV where it can be complicated and mysterious, so much so that Rob Richie, the USA's foremost IRV advocate, got it wrong in his only scientific publication, then got it wrong some more.
If you agree with our "probably more often," then Richie's claim this issue leads us "back toward plurality voting dynamics" was probably exactly the opposite of the truth. Also, this whole issue favors approval voting versus IRV, even though Richie makes it sound like the opposite. So to review:
| Voting method | "Honesty re Favorite" is safe? | "Honesty re 2nd-Favorite" is strategically safe? | Voting never worse for you than not voting? | How hard to assess? |
|---|---|---|---|---|
| APPROVAL VOTING | Yes. Always. | Could be mistake to approve 2nd-fav; also could be mistake to disapprove (probably latter happens more often). But either way, you have not yet been forced to lie. (Which is good for society, since lie-votes tend to diminish the quality of the winners a voting system chooses.) | Correct. | Straightforward. |
| IRV (Richie's favorite) | No. | No (i.e. same situation as for approval, except worse in sense voter may be forced to lie about her 2nd favorite). | No. | Too hard for Rob Richie, USA's foremost IRV propagandist, even to recognize these problems exist for years. (Although these were well known to voting theory community.) |
A voting system even more favored by Richie's "second favorite" issue would be score voting, since in Approval voting, if you approve your second-favorite, then you effectively rate him equal to to your genuine favorite. With score voting, you could rate him (say) "only 90% as good" (or whatever number you like). But as both the table and real life experience shows, even approval voting (which makes no attempt whatever to allow that) still seems, if anything, superior to IRV on this issue.
And that is true even with election data specifically cherrypicked by Richie himself to make approval look maximally bad (if we use the correct data)!
But for the purposes of argument, let's suppose Richie's utterly false Colorado claims actually had been true. Even then – so what? Richie would then be complaining that "A beat B by 51.9% to 51.6% approval, but really maybe B should have won because 3% of the voters approved both, whereas really maybe they would have split 60:40 in favor of B if they hadn't been so confused by the horribly hard-to-fathom approval system." (Actually zero out of 6686 voters were thus-confused, but Richie is very fearful about that confusion. The genuinely-confusing behavior of IRV, and the immensely complexity of official IRV election-worker instructions, and the fact that spoiled ballot rates decrease with approval but increase with IRV, apparently bother him much less.) With Richie's postulation, B should have beaten A by 53.8 to 53.3 so democracy was denied. Was this a disaster? Hardly. This was "an extremely close election" so swinging it is a very tiny denial of democracy. In contrast, the Australian House, elected by IRV, failed to elect even a single third party candidate in 3 election cycles in a row (2001, 2004, 2007) which perhaps is why Australians want to get rid of it. Now that is a denial/distortion of democracy causing far more damage.
It is rather revealing that even Rob Richie, the foremost IRV propagandist in the USA, after decades of professional experience and the beneficiary of millions of dollars in funding, was unable to produce an anti-approval pro-IRV argument better than the one at top (even with thousands of dollars at stake).