D-dimensional orderings and Stirling numbers

By Warren D. Smith, October 2014.

ABSTRACT. We find the maximum, and generic, number of "orderings" of N points in D-dimensional space, provided the points are ordered by increasing distance from another (movable) point, or along a (movable) direction. We also find asymptotic formulas for these quantities, and for Stirling numbers of both kinds, along any ray in the (N,D) parameter-plane.

Statement of our two problems

Let there be N "candidates," who each are distinct points in D-dimensional "issue space."

1. Let a "voter" be another point in D-space, and assume any voter rank-orders the candidates by distance from her (nearer candidates preferred). Define R(N,D) to be the maximum (or generic) number of different orderings that could arise as the position of the voter is varied.
2. Define Q(N,D) to be the maximum possible (or generic) number of honest linear-orderings of those candidates under different directional preferences. In this model, a "voter" instead is a direction (unit length D-vector) and the ordering is of the candidates in that direction, i.e. by their dot-product with that direction.

The problems are to understand R(N,D) and Q(N,D).

Notes: "Orderings" that include ties are ignored. The number of orderings which arises when the N candidates are generic points, i.e. whose coordinates disobey every non-identity multivariate polynomial equation with integer coefficients, is one problem, and the maximum number (maximized over all N-point sets in D-space), is a different problem – so really we have 4 problem versions. It is not immediately obvious the generic and maximum numbers are always the same, but we will prove they are. It also may not be immediately obvious any single-valued "generic" count always exists – but it does, as we'll also prove (e.g. it eventually will become obvious once you know Zaslavsky's theorem; also follows from our proof of the fundamental recurrences). It indeed will turn out that we could have permitted the candidates to lie in any higher dimensional space (say D+Δ dimensional for Δ≥0) provided the voter still is demanded to lie in D-space; the answer-counts are not affected by this change in the problem definition.

Of course R(N,D)≥Q(N,D)≥1, indeed Q(N,D) arises from the R(N,D) problem by insisting the voter lie on the "sphere at infinity." The ultimate level of understanding would be to find exact formulas for them, but one also could just find upper & lower bounds. We are going to find exact formulas. We also shall find somewhat simpler upper bounds (valid for the "maximum" versions) which are asymptotically tight when N→∞ with D fixed.

These problems can be regarded as fundamental problems in political science, and also have interest in combinatorial geometry.

Obviously R(N,D)=Q(N,D)=N! if D is made sufficiently large with N fixed. But when D is fixed and N grows large, it is interesting and important that there are far fewer "D-dimensional orderings" than the total number N! of possible orderings of N items.

These problems, and their solution, are (mostly) not new!

A funny thing happened after I wrote the first draft of this paper. Richard P. Stanley pointed out Good & Tideman 1977, which solves my same R(N,D) problem expressing it as a certain sum of "Stirling numbers of the first kind." It seemed to me their proof might not be fully rigorous (there were several fine points they'd blissfully ignored) but basically they'd "scooped" me 37 years prior. Tideman then recommended the followup paper Zaslavsky 2002. Zaslavsky redid the Good-Tideman proof his own way (he also had some criticism of it but which, he ultimately concluded, does not matter in the sense that Good & Tideman's answer still comes out correct), also with a more general result. Zaslavsky claims, now using Mathematica's notation for Stirling numbers, that

By agreeing (as is standard) that if N-k is negative then the StirlingS1 equals zero, the problem is avoided that Zaslavsky's sum would otherwise become undefined when N<D.

Then I worked harder at literature searching and found Cover 1967, which had scooped me even earlier by solving the Q(N,D) problem! Cover found the recurrence

which together with the base cases that Q(N,D)=N! if N≤D+1 and Q(N,1)=2 if N≥2, suffice to fill the whole Q-table. Incredibly enough, I then observed empirically that the exact same recurrence as Cover's for Q(N,D), also is obeyed by R(N,D) – albeit since the first row of the R-table is different from the first row of the Q-table, we do not get the same tables. [We later will present an extremely simple proof of both Cover's and my new recurrence; which also shall show they solve both the "generic" and "maximum" problem versions. The previous authors had only considered "generic," except for Edelsbrunner for Q(N,2).] Specifically: The way I have laid out these tables, the recurrence determines each table-entry from the entry immediately above and the one immediately leftward, for example 16369178=4496284+11×1079354 highlit yellow above. The leftmost column of each table is trivially found since it just consists of factorials. The top row of each table also is given by a simple formula: Q(N,1)=2 if N≥2, and R(N,1)=(N-1)N/2+1. Actually we could, if desired, also define R(N,0)≡1 and then the recurrence still would hold in the thus-extended R-table.

I think I should be forgiven for rediscovering all this, because the authors of the original papers I worked in blissful ignorance of, also mainly were unaware of each other. Zaslavsky 2002, and Good & Tideman 1977, were unaware of Cover 1967. Edelsbrunner 1987 [who in his book solved the Q(N,2) problem], and the "geometric k-sets" literature in general, seemed unaware of either; and Orlik & Terao in their 1992 book putatively summarizing the entire area, didn't mention any of them. Nor was the poser (to me in 2014) of these problems, David W. Wilson, aware of any of them. Hence it would not surprise me if even more discoverers exist. Indeed, I then found Gould 1974, who used Cover 1967 to show

where the sum alternatively may be taken to be over all non-negative integer j under the convention that StirlingS1(N,K)=0 if N<K. Gould's referee pointed out that Cover's recurrence relation had been discovered (without proof) by Bennett 1956, who probably would have done more if he had not died in that same year. The StirlingS1's are fundamental combinatorial quantities and may be defined as StirlingS1(N,K)=(-1)^N+K times the number of permutations of N objects having exactly K cycles. [In fact, as better names, Knuth recommends calling them "Stirling cycle numbers" and for Stirling numbers of the 2nd kind, the corresponding better name is "Stirling subset numbers."] They may be computed from the recurrence

with base cases StirlingS1(N,K)=0 if either K>N, K≤0, or N=0; except for Stirling(0,0)=1. Also StirlingS1(N,1)=(-1)^N+1(N-1)!, StirlingS1(N,1)=(-1)^N(N-1)!H_N-1, StirlingS1(N,N)=1, and StirlingS1(N,N-1)=(1-N)N/2. When I finally became aware of all that, I was able – suddenly with a full view of the situation and everybody's ideas – to simplify and/or generalize their results. I then entirely rewrote the present paper.

Although the closed form expressions of Q(N,D) and R(N,D) as sums of Stirling numbers were rather mysterious to their original discoverers, they now are trivial to derive from the fundamental recurrences for Q and R and StirlingS1. They are not terribly directly useful, indeed it seems easier to go in the other direction by computing StirlingS1 from R:

The real benefit is that the wealth of knowledge about (e.g. asymptotics and identities involving) Stirling numbers can then be quickly translated into knowledge about Q(N,D) and R(N,D). For example, known "generating functions" for the StirlingS1's include

Using the top right identity, it is not hard to find these generating functions:

A little Terminology & Background

Let VoD stand for Voronoi diagram. The all-orders Voronoi diagram of N points in D-space (AOVoD) shall mean the arrangement of the H=(N-1)N/2 hyperplanes that are perpendicular bisectors of the line segments whose endpoints are two distinct points within our set of candidates.

It is a useful and fairly well known fact that the number A(H,D) of cells in an arrangement of H generic hyperplanes in D-space (this formula also gives the maximum possible number of cells, maximized over all possible such hyperplane arrangements, i.e. for this cell-counting problem, the generic and maximum values are equal) is

Also, the number of infinite cells in this arrangement is (both generically and maximally)

One proof is via Zaslavsky's theorem discussed below. But that is overkill. A different proof is to note the recurrence A(H,D)=A(H-1,D)+A(H-1,D-1) holds generically and maximally. This arises by considering adding hyperplane H to the arrangement formed from hyperplanes 1,2,3,...,H-1. Note the arrangement intersected with this new hyperplane is a (D-1)-dimensional arrangement and its cell-count is the number of cells of the D-dimensional arrangement that are split by the new hyperplane. The base cases are A(1,D)=2 when D≥1, and A(H,1)=H+1. All these base and inductive cases obviously hold both generically and maximally. We then may show the sum-of-binomials formula satisfies them all. Also, A_∞(H,D)=2A(H-1,D-1) arises by replacing the "sphere at infinity" by two suitable hyperplanes parallel to one of the original ones (these exist if H≥1 and D≥1) but very far away (this does not change the count of infinite cells), and considering the (D-1)-dimensional situation on those hyperplanes only.

Connection of our problems to all-orders VoD

Further, by constructing the AOVoD you can actually algorithmically determine all these orderings for any particular N-point set. One ordering corresponds to each cell in the arrangement (voter can be located anywhere in that cell); for the Q(N,D) problem only the infinite cells matter. If D is fixed, N large, then (we'll see) the run time is proportional to their number if Edelsbrunner 1987's arrangement-constructing algorithms are used.

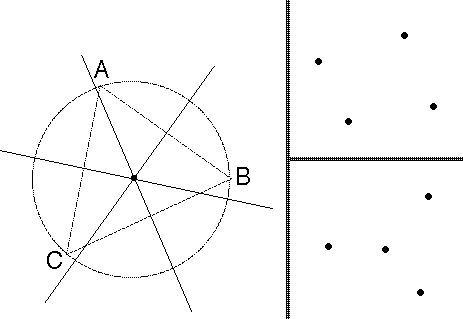
Oddly enough, although the number of orderings remains unchanged as the N points are moved (provided the motion keeps them generic), the set of these orderings can change. This is demonstrated by the right half of the figure below (due to Cover for the Q-problem).

Figure: At left: the three perpendicular bisector lines of points A,B,C coincide at the triangle's circumcenter. At right: two generic 4-point sets. Each shows R(4,2)=18 and Q(4,2)=12, but the set of 12 linear orderings for the top point set differs from the set of 12 for the lower set (no matter how the points are labeled); and similarly the set of 18 distance orderings for the top point set differs from the set of 18 for the lower set. To see that, note that in the top set, all 4 points can be at either extreme end of the ordering, but in the bottom set, the middle point cannot be extreme in any linear ordering, and cannot be furthest in any distance ordering.

Direct solutions in some small dimensions D (or for small numbers N of points)

Because: There is exactly one ordering of N=0 or of N=1 candidates.

Because: If the N points form a regular simplex (or any nearly-regular simplex) then by symmetry any ordering is achievable. And we'll later see (e.g. from Zaslavsky's theorem) that the values of Q(N,D) and R(N,D) are the same for any generic N-point set as for any other.

Because: If the N points form a regular simplex (or any nearly regular simplex) plus its centerpoint (or near-enough point to the center) then by symmetry any ordering is achieveable for the D+1 simplex vertices. However, for Q(N,D), the centerpoint lies strictly inside the convex hull of the other points, hence cannot be one of the two extreme points of the ordering. It should be obvious it can be any other, though. So we do not get (D+2)!=(D+1)!(D+2), but rather only (D+1)!D orderings. For R(N,D), the centerpoint can be made first (nearest to the voter) in the ordering by placing voter nearby to it. But it cannot be made last. Hence we do not get (D+2)!=(D+1)!(D+2), but rather only (D+1)!(D+1) orderings.

Because: The forwards & backwards ordering of the candidates along the real line.

Because: the all-orders-VoD is delineated by (N-1)N/2 candidate-pair-midpoints, which generically all are distinct.

Because the all-orders-VoD infinite regions are got from the (N-1)N/2 point-pair-bisector lines intersecting the "circle at infinity." Each line has two endpoints at infinity, and all line-slopes are generically distinct hence all endpoints distinct. These endpoints partition the circle at infinity into the same number of arcs, except if 0 endpoints then 1 arc (the whole circle).

generically. The following demonstration does not make it clear it also is maximum. Proof: Each 3-tuple of points has a (generically distinct) circumcenter where their three point-pair-bisector lines concur. The intersection points of the lines therefore consist of (N-2)(N-1)N/6 points where we have 3-line-concurrences, plus (N-3)(N-2)(N-1)N/8 points where we have 2-line concurrences. So there are

vertices in the all-orders-VoD line-arrangement, all generically distinct, and this is maximal. Each line contains N-2 vertices that are 3-way plus (N-2)(N-3)/2 that are 2-way, for, in all, (N-1)(N-2)/2 vertices on each line, all generically distinct. There are (N-1)N/2 point-pair bisector lines, all generically distinct. Hence the whole AOVoD can be regarded as a polyhedral planar graph with

vertices (note I have added one additional vertex at infinity) and

edges. One can also compute the number E of edges in a different way using 2E=∑(valencies), finding

Hooray, these two calculations of E agree. Hence using Euler's polyhedral formula V-E+F=2 the number of faces (cell regions) is

using the first E formula (the second of course yields the same result). For N=0,1,2,3,4,5,6,7,8,9 these yield F=1,1,2,6,18,46,101,197,351,583 which I verify are correct for N=0,1,2,3 at least. [Incidentally F=1,1,2,6 would agree with the cubic formula (N+1)(2N²-5N+6)/6 for N=0,1,2,3 but not with any quadratic and would continue F=1,1,2,6,15,31,56,92,141,205,... but this of course is wrong when N≥4.]

generically. The following demonstration does not make it clear it also is maximum. Proof: (You will need to understand the preceding derivation of R(N,2) since we now are going to go a bit quickly for those who haven't understood that.) On the sphere at infinity, we want to know the number of faces in arrangement got from the H=(N-1)N/2 point-pair-bisector great-circles. There are (N-2)(N-1)N/3 vertices where 3 circles coincide. There are (N-3)(N-2)(N-1)N/4 vertices where 2 coincide. Each circle has 2(N-2) vertices on it at which 3 circles coincide, plus (N-2)(N-3) vertices on it at which 2 circles coincide, for (N-2)(N-1) in all on each circle. Hence we have a planar graph drawn on the sphere at infinity with V=(N-2)(N-1)N/3+(N-3)(N-2)(N-1)N/4=(N-2)(N-1)N(3N-5)/12 vertices and E=(N-2)(N-1)²N/2 edges. Hence the number of faces F is

This yields F=2,2,2,6,24,72,172,352,646,1094 for N=0,1,2,3,4,5,6,7,8,9. Those F-numbers are wrong for N=0 and N=1 (then really F=1) because Euler's formula V-E+F=2 is not applicable when V=E=0.

Some easy upper bounds, valid in all dimensions D≥1

We shall see later that these upper bounds are asymptotically tight when N→∞ with D≥1 fixed, since the exact Q(N,D) and R(N,D) formulas also are polynomials in N, of the same degree, and with the same leading term.

Proof of the fundamental recurrences

We'll first prove them for generic point sets. If you add an (N+1)st candidate-point, then N new candidate-pair-bisecting hyperplanes spring into being. On each, there is a (D-1)-dimensional arrangement arising from the old N candidates, but the N candidates need not lie on that (D-1)-dimensional hyperplane, they lie in D-space. This "but," however, generically does not affect either cell counts, or infinite-cell counts, as you can see from a perturbation argument considering moving those N candidate-points from on that (D-1)-dimensional hyperplane, to being a little off it in D-space. So on each of these hyperplanes, the old N candidates generically split that (D-1)-space into R(N,D-1) cells with Q(N,D-1) of them being infinite cells.

Furthermore, of these N new hyperplanes, each two of them intersect in a (D-2)-dimensional flat, which nowhere intersects the interior of any cell of the old (original N candidates) partitioning of D-space. That is because, if it did at some point X, then X would be equidistant from (say) candidates N+1 & 1, and simultaneously from candidates N+1 & 2, but not equidistant from candidates J & K for any 0<J<K≤N. But actually, a diagram drawn in the 2-dimensional plane (circumcenter of triangle 1, 2, N+1; see left part of figure above) shows that equidistance from 1 & 2 is then forced.

This "nowhere intersects cell interiors" property causes each of these N new hyperplanes to split different cells only – my point is the different hyperplanes do not interfere with each other, so we can just sum their counts of split cells! Hence voila: we have proven these recurrences: if N≥2 then

the rightmost terms arising from the cell-splittings by the N new hyperplanes, and the left terms on the right hand sides being from the old situation with only N candidates.

These recurrences, plus the known values of R(N,D) and Q(N,D) when N≤2 or D=1, are all one needs to completely solve both the R(N,D) and Q(N,D) problems in all dimensions.

The above has been a simplification and generalization of Cover 1967's Q-argument. We now note that the same proof also proves the recurrences for the maximum problem versions. To see that, first of all the base cases R(N,D)=Q(N,D)=N! if N≥D+1, and R(N,1)=2 and Q(N,1)=(N-1)N/2 are maximal – the first since N! is the most orderings there could be, the second we already proved. And now our inductive recurrence is maximal because the most we could hope for is that the cell-splitting counts for all N new hyperplanes sum (which they do) and that on each we have a maximal-cell-count (D-1)-dimensional diagram. This is true by induction on D, using a slight redefinition of all our problems throughout, in which we allow our N candidate-points, but not the voter, to lie in a higher dimensional space. Q.E.D.

The remaining formulas in dimensions D≤5

The fundamental recurrences allow one to induct formulas for R(N,D) and Q(N,D) for each D successively. We continue up to D=5:

If one performs the same induction worrying only about the leading term, then we see that

Probabilistic and "coin flipping" interpretations

|StirlingS1(N,K)|/N! is the probability that a random permutation of N items has exactly K cycles. Also, after independently tossing N-1 coins with head-probabilities 1/2, 1/3, ..., 1/N, then |StirlingS1(N,K)|/N! is the probability that exactly K-1 heads arise. Equivalently, if we toss N coins with head-probabilities 1, 1/2, 1/3, ..., 1/N, then |StirlingS1(N,K)|/N! is the probability that exactly K heads arise.

The probability R(N,D)/N! that a random N-permutation arises as a distance order, equals the probability that there are ≥N-D heads (equivalently ≤D tails) in N independent flips of coins having individual probabilities of heads 1, 1/2, 1/3, 1/4, ..., 1/N. Also, it equals the probability that a random permutation of N items has ≥N-D cycles.

The probability Q(N,D)/N! that a random N-permutation arises as a directional order, equals the probability that there are ≥N-1-D heads (equivalently ≤D-1 tails) in N-2 independent flips of coins having heads-probabilities 1/3, 1/4, 1/5, ..., 1/N. Also, it equals the probability that a random permutation of N items has ≥N+1-D cycles and that this number of cycles has the same parity (odd or even) as N+1-D.

All these statements are easy consequences of staring at the generating function and/or Stirling-number-sum identities, and Cover 1967 had already noticed some version of one of the ones for Q(N,D).

Zaslavsky's theorem

When D≥3 or 4, our preceding low dimensional solution methods which relied on Euler's polyhedral formula, stop working. This is because Euler's theorem stops existing, or anyhow loses power, in higher dimensions.

One could solve the problem for any D by using Zaslavsky's 1975 theorem for counting cells in an arrangement of H=(N-1)N/2 hyperplanes in D-space. This method is more difficult than using the fundamental recurrence. But let us briefly consider it anyhow. The difficulty is that our H hyperplanes are not generic, hence the generic counting formula we called A(H,D), cannot be used (although it is valid if all we want is to find upper bounds). Zaslavsky's theorem will, at least in principle (the details could, in practice, sometimes be too hard to deal with) count the cells in any arrangement of hyperplanes whose "poset structure" is understood.

In what way are our H hyperplanes non-generic? The "circumcenter" of a triangle, is the intersection of the perpendicular bisectors of its 3 sides. More generally the circumcenter of a D-dimensional simplex (which has D+1 corners) is the unique intersection of the perpendicular bisectors of its (D+1)D/2 sides. In our set of H hyperplanes we therefore get concurrences of (D+1)D/2 hyperplanes at common points (namely, the circumcenter-points of any subset of D+1 of our candidate-points) which is way more than the concurrences, of only D hyperplanes, that are the most that ever happen for a generic hyperplane set. Furthermore, we have for example when D=3, that often 3 hyperplanes concur on a common line.

What is the "poset structure" of a set of H hyperplanes? Let L denote the set of subsets of our hyperplane set, having non-empty intersection. (Sometimes L is called "the intersection lattice" although I do not like to employ the word "lattice" in this way; I think it was a poor name-choice.) These subsets enjoy a partial order under the set-inclusion operation ⊆. For example, if hyperplanes 1,2,3,4 all intersect at at least one common point, then {1,2,3,4}∈L, and hence {1,2,4}∈L also. And {1,2,4}⊆{1,2,3,4}. A "poset" is a set having a partial order defined on it, so L partially ordered via ⊆ is a poset, called "the poset structure of our hyperplane set."

Thomas Zaslavsky commented "There is reason to order the intersection subspaces oppositely to how you do it, i.e., the reverse of set containment." Actually, I did not say "which direction" I intended the order to be in – although the reader might naturally guess that the ⊆ and usual ≤ symbols should point the same way – and this directionality does not actually matter for my purposes in the sense that our definition of the Möbius function is unaffected by it. Zaslavsky's direction-preference, therefore, is motivated by issues that do not matter for our purposes here.

What is the Möbius function μ(x,y)? When x∈L and y∈L then μ(x,y) is the unique function obeying

One can compute the Möbius function from these equations (regarding them as recurrences) by starting from μ(x,x)=1 and using

What is "Zaslavsky's theorem"? It states: The number of regions into which D-space is split by the arrangement of hyperplanes can be found by summing the absolute values of Möbius function values for the corresponding L:

Here ∅ denotes the empty set, which we regard as an honorary member of L.

Example: The formula we gave previously for A(H,D) then follows immediately once you work out that ∑|μ(∅,x)|=H!/[(H-K)!K!] where the sum is over x that are sets of exactly K hyperplanes where 0≤K≤D. (If K≥D+1 then x∉L.)

What about counting only the infinite cells in a hyperplane arrangement? There is a variant Zaslavsky theorem for this purpose. It uses L_∞, the "unbounded intersection lattice," instead of L, e.g. see Ehrenborg, Readdy, Slone 2009.

For us, the most important realization from Zaslavsky's theorem is

The lack of geometric magic in the world

It is mildly magical that the (D+1)D/2 point-pair-bisector hyperplanes of D+1 points in D-space, all concur (at the circumcenter of the simplex). One might wonder whether, given N generic points in D-space, there could be any further magic. Maybe a "bipyramid" yields some additional hyperplane concurrence, in some dimension – or something?

Well, that does not happen: Geometric fact: For N generic points in D-space, there is nowhere where more than D of their point-pair-bisector hyperplanes concur, except for the already-known concurrences arising from simplex circumcenters.

This is because, if even a single such extra concurrence-point existed in any dimension anywhere, it would via Zaslavsky's theorem alter the generic value of some Q(N,D). Which we know does not happen.

Asymptotics

We've seen that when D≥N-1, then R(N,D)=Q(N,D)=N!, but when D≤N-2, then R(N,D)<N! and Q(N,D)<N!.

Question: How large does D have to become to cause R(N,D) and Q(N,D) to reach the same order as N!  ?

This is related (via Stirling number sum identities) to various classical facts. The expected number E(C) of cycles in a random permutation of N items, is exactly

because the expected number of cycles of length ≤m equals H_m if 1≤m≤N. Another, even easier, proof arises from the coin-flipping interpretation, which also shows

"Goncharov's theorem" states that in the limit N→∞, the probability distribution of C, namely prob(C)=|StirlingS1(N,C)|/N!, tends to a normal distribution with this mean and variance. Goncharov 1944's own derivation was brutal, but his result actually can be proven trivially from our coin flipping interpretation using the Lindeberg form of the central limit theorem from statistics.

That proves the result. But we also note that those all correspond to certain identities for StirlingS1 numbers, e.g. EQs 6.14 & 6.28 in the manuscript of Gould & Quaintance. Also, the following two identities were stated without proof by Terence Tao (they should be provable using the automated techniques of Kauers 2007): E(2^C)=N+1 and indeed for any fixed integer M≥1 we have E(M^C)=(N+M-1)!/[N!(M-1)!]; these seem not yet present in the Gould-Quaintance compilation. Louchard and the papers he cites go considerably beyond this result, finding StirlingS1(N,K) asymptotics for K near both ends of the interval [0,N].

Question: What if N and D grow proportionally (like D≈cN for some constant c with 0<c<1) when N→∞?

Answer:   Then R(N,D), Q(N,D-1)/2 and |StirlingS1(N,N-D)| all are bounded between two expressions of the form k^DD! where the k's with 0<k depend upon c and the difference between the two k's may be made arbitarily small. These claims may be proven, for example, by showing a lower bound by simply counting the number of permutations of N items having N-D cycles, all cycles having as nearly equal cardinalities as possible; and an upper bound in a similar way also using subexponential upper bounds on the number of partitions of N. I then conjectured, more precisely, that these all simultaneously ought to be asymptotic to

for appropriate constants m,j,k which depend upon c; I found the formulas:

where the "-1" subscript denotes the lower branch of the Lambert W function. Actually since j=-1 we may state these formulas in the slightly simpler form

I did not carefully check either the complicated algebra or that the manipulations I performed genuinely are a proof. Nevertheless, numerical checks suggested these j,k,m formulas all are correct:

• With c=0.1 we find L≈1.10714650294425, k≈344.818640511284, m≈0.15375566682 whereupon taking N=990, D=99=cN, N-D=891, we find (D-1)!k^Dm≈2.4137×10⁴⁰⁴ which is 1.0017 times greater than the exact absolute value of StirlingS1(990, 891)≈-2.40959×10⁴⁰⁴.
• With c=0.5 we find L≈1.75643120862617, k≈9.82162992913651, m≈0.129395869881879 whereupon taking N=600, D=N-D=300=cN, we find (D-1)!k^Dm≈5.96585×10⁹⁰⁸ which now is within a factor 1.001 of the exact StirlingS1(600,300)=5.96049×10⁹⁰⁸.
• Finally with c=0.9 we find L≈3.71495042708753, k≈1.70626857427758, m≈0.09163479957745, whereupon taking N=1000, D=900=cN, N-D=100, we find (D-1)!k^Dm≈4.78572×10²⁴⁷⁴ which is off by about a factor 1.003 versus the exact StirlingS1(1000,100)=4.771093×10²⁴⁷⁴.

This asymptotic formula for Stirling numbers was not mentioned in the NIST Digital Library as of 2014, nor in Temme 1993. However, I found certain special cases of this formula stated in the The On-Line Encyclopedia of Integer Sequences, for example sequences A187646 & A237993, ascribed to Vaclav Kotesovec, May of 2011 & 2014 respectively. And then some googling found that Kotesovec stated in passing (without any indication of proof) asymptotic approximations for both StirlingS1 and StirlingS2 numbers, which appear (according to numerical checks) to be essentially equivalent to mine here, in the midst of a 2013 manuscript he'd posted on his web page. After email enquiry, Kotesovec explained that his StirlingS1 formulas were derived from Good 1961 and his StirlingS2 formulas from Timashev 1998, neither of which had been cited by the NIST digital library! Good's method of derivation (saddlepoint method via the log-based generating function), and his result, both are essentially equivalent to mine. Good indeed explains how to obtain higher-order correction terms. Also deriving essentially the same result: Knessl & Keller 1991, and Moser & Wyman 1958. The latter claimed that their |StirlingS1(N,N-D)| asymptotic should be valid when (N-D)/ln(N)→∞ with D>N^P for any fixed power P with 0<P<1, which note is a wider domain of validity than my demand (also stated by Good and Knessl) that c be fixed with 0<c<1. Moser & Wyman also gave |StirlingS1(N,N-D)|∼Binomial(N,D)([N-D]/2)^D when D=o(√N) and N→∞; and |StirlingS1(N,K)|∼(γ+lnN)^K-1/(K-1)! when N→∞ with K=o(lnN) where γ=0.57721... These all leave only the domain where D/ln(N) remains bounded between two positive numbers while N→∞ uncovered. But this missing domain is more than handled by Goncharov's theorem.

Similar asymptotics for Stirling numbers of the 2nd kind, and Binomial coefficients

These results are not directly relevant to our topic, but since we are here, we might as well also provide asymptotic formulae for these too. StirlingS2(N,M) is the number of partitions of N distinguishable items into exactly M nonempty sets. Special values: StirlingS2(N,0)=0, StirlingS2(N,1)=StirlingS2(N,N)=1, StirlingS2(N,2)=2^N-1-1, StirlingS2(N,N-1)=(N-1)N/2. Recurrence:

One may show directly from Temme 1993 EQs 2.6, 2.8, 2.9, and 2.10 using n=N=D/c, m=N-D, t₀=c/(1-c) and x₀=(1-c)^-1+LambertW(-e^-1/(1-c)/[1-c]) in his notation, that

where now the formulas for j and k are

This is essentially equivalent to Temme's result about StirlingS2 albeit considerably nicer because Temme gave this result in an unappetizing unsimplified form, distributed over several pages. It indeed should be valid when min{N,N-D,D}→∞. Here are some numerical checks with N=450:

Also of interest are the numbers STS(N,K)=∑_1≤j≤KStirlingS2(N,j) giving the number of ways to partition N distinguishable items into M or fewer nonempty sets. These obey those same asymptotics as StirlingS2. Special values include STS(N,0)=0, STS(N,1)=1, STS(N,2)=2^N-1, STS(N,N)=BellNumber(N). Recurrence:

We also mention that Stirling's formula easily shows the asymptotic

What was that LambertW function?

LambertW(x) is the solution W of We^W=x. If x<-1/e≈-0.3678794 no real solution exists. If 0≤x a real solution does exist, and it is unique, positive, and increasing. If -1/e<x<0 then there are two real solutions; the unique solution W with -1<W<0 (which is a smooth continuation of the solution for x≥0), and the other solution which obeys W<-1. This "lower branch" is denoted LambertW_-1(x). Special values include LambertW(-1/e)=LambertW_-1(-1/e)=-1, LambertW(0)=0, LambertW(e)=1. If x≥-1/e the following algorithm

 if(x < 3.5){
    if(x < -0.2114){ W ← (5.43656·(x+1/e))1/2 - 1; }
    else{ W ← x/e; }
  }else{ W ← ln(x); E ← ln(W); W ← W-E+E/W; }

outputs an approximation W to LambertW(x) which is good enough both to have uniformly bounded relative and additive errors, and (if used as a starting guess) to assure global convergence of the iteration

(On my computer at most 6 iterations are required to reach full machine precision.) If -1/e≤x<0 then the following algorithm

  if(x < -0.283){ W ← -(5.43656·(x+1/e))1/2 - 1; }
  else{ W ← ln(-x); E ← ln(-W); W ← W-E+E/W; }

outputs an approximation W to LambertW_-1(x) which is good enough both to have uniformly bounded relative and additive errors, and again to assure global convergence of that iteration.

Algorithmic complexity

The fundamental recurrences make it trivial to compute a table of the R(N,D) and Q(N,D) functions (laid out like my tables above) in O(1) arithmetic operations per table entry; the tables can be filled in row-by-row, column-by-column, or by successive /-diagonals.

But suppose that we want, not the entire table, but rather only a single /-diagonal of it. By using our previous nifty generating function identities, multiplying the terms in the fashion of a balanced binary tree, and using FFT-based fast polynomial-multiplication algorithms, it is possible to compute Q(N,1), Q(N,2), ..., Q(N,D) or R(N,0), R(N,1), R(N,2), ..., R(N,D) (combined) in O(D+N(logN)²) arithmetic operations and storage for O(N) numbers. Further, if we only keep track of powers≤D of t in the generating functions (regarded as formal power series in t) throughout this process, then it takes only O(N(logN)(logD)) arithmetics and storage for O(D) numbers. All these same algorithmic bounds also hold for Stirling numbers of the first and second kinds, which is a fact that ought to be in all the textbooks, but isn't. It also is possible to compute StirlingS1(n,K) for all n=0..N simulataneously using the log-based generating function with powers≤N only, and StirlingS2(n,K) similarly using the exp-based generating function (EQ 26.8.12 in the NIST digital library), in O(NlogNlogK) arithmetic operations. These op-counts eventually are much smaller than order DN, which is the number of arithmetics the naive method based on the fundamental recurrences would consume. And now suppose we want only a single row of the Q- or R-table. We claim it is possible to compute the first T entries of row D of the table in O(TlogD+D²) arithmetic operations while storing O(D) numbers. [Compute the first 2D+1 entries of the row by the fundamental recurrence in O(D²) arithmetics and O(D) numbers storage, then Newton-interpolate by a polynomial(N), then employ algorithms for "fast multipoint polynomial evaluation" on arithmetic progressions, see Bostan & Schost 2005.] Now because either N≤D+1, in which case R(N,D)=Q(N,D)=N! is computable in N arithmetic operations, or D+2≤N≤(D/logD)², in which case use the D(logN)(logD) algorithm, or N≥(D/logD)² in which case use the fundamental recurrence, Newton-interpolation, then evaluate the polynomial(N) at one single N, we find:

Questions

Are our algorithmic complexity bounds best possible? Obtain better understanding of the asymptotics of R(N,D) and Q(N,D).

Acknowledgments

David W. Wilson suggested the problems and found Q(N,2). Tom Rokicki found Q(N,2), which also was basically shown in chapter 2 of the 1987 book by Edelsbrunner under the name "circular sequences." J.P. Grossman found Q(N,3). Rokicki & Grossman could be regarded as having worked independently from me, so we confirm each other's results. Eric Michael Samansky, while an undergrad at Haverford College (as of 2014 he is an associate professor at Nova Southeastern Univ.) wrote a highly readable exposition of Zaslavsky's theorem which I've leaned on heavily. It uses the notion of "Möbius functions of posets" which is explained in chapter 26 of the 1978 book by Nijenhuis & Wilf. Richard P. Stanley pointed out Good & Tideman 1977, then Tideman pointed out Zaslavsky 2002. Finally Zaslavsky sent me some comments. One of his best was:

The Stirling numbers s(n,k) arise naturally in this problem for the following reason: the intersection poset (ordered my way) consists of the lower D+1 levels of the lattice of partitions of the set of candidates. That is what my proof brings to the fore and it fully explains the Stirling number formula (to me, anyhow).

After I discovered the Stirlng number asymptotic formulas given here, I thought they were new since not mentioned in the NIST digital library. We've explained how Vaclav Kotesovec pointed me toward finding out that they were not new. Actually, I still have not seen asymptotic formulae as simple as mine anywhere(?), but they evidently are equivalent to formulae discovered previously by others and expressed in more complicated ways.

Relevant References

Richard Arratia & Simon Tavare: The cycle structure of random permutations, Annals Probab. 20,3 (1992) 1567-1591.

Joseph F. Bennett: Determination of the number of independent parameters of a score matrix from the examination of rank orders, Psychometrika 21,4 (1956) 383-393.

L.J. Billera, R. Ehrenborg, M. Readdy: The c-2d-index of oriented matroids, J. Combin. Theory Ser. A 80 (1997) 79-105.

Dario Bini & Victor Pan: Polynomial and Matrix Computations, Vol 1: Fundamental Algorithms, Birkhauser, Boston 1994.

W.E. Bleick & Peter C.C. Wang: Asymptotics of Stirling numbers of the 2nd kind, Proc. Amer. Math'l. Soc. 42,2 (Feb. 1974) 575-580. Erratum: 48,2 (1975) 518. They used the saddle point method on the exp-based generating function to find an asymptotic expression for StirlingS2(N,K) which works excellently for all K with 2≤K≤N-1. This expression (including two subleading terms) is their EQ21 on page 579 (but correct it by changing the sign preceding the last fraction in the bracket from + to –!) using (N+1)/K=u/(1-e^-u)=e^uG so that u=t+LambertW(-e^-tt) with t=(N+1)/K. Note that t>1 and t-1<u<t and G>0. The leading term of this is

A.Borodin & R.Moenck: Fast modular transforms, Journal of Computer & System Sciences 8 (1974) 366-386.

Alin Bostan & Eric Schost: Polynomial evaluation and interpolation on special sets of points, J. Complexity 21,4 (Aug. 2005) 420-446.

E. Rodney Canfield: On the location of the maximum Stirling number(s) of the second kind. Studies Appl. Math. 59,1 (1978) 83-93.

Thomas M. Cover: The number of linearly inducible orderings of points in d-space, SIAM J. Applied Maths. 15,2 (March 1967) 434-439.

Priyavrat Deshpande: On a Generalization of Zaslavsky's Theorem for Hyperplane Arrangements, Annals of Combinatorics 18,1 (March 2014) 35-55.

Herbert Edelsbrunner: Algorithms in combinatorial geometry, Springer 1987.

Richard Ehrenborg, Margaret Readdy, Michael Slone: Affine and toric hyperplane arrangements, Discrete & Computational Geometry 41,4 (2009) 481-512.

Pal Erdös: On a conjetcure of Hammersley, J. London Math'l Soc. 28 (1953) 232-236.

Irving John Good: An Asymptotic Formula for the Differences of the Powers at Zero, Annals of Mathematical Statistics 32,1 (1961) 249-256. [Asymptotics of Stirling numbers of the first kind in §4.]

V.Goncharov: Du domaine d'analyse combinatoire, Bull. Acad. Sci. USSR Ser. Math. 8 (1944) 3-48. [Russian with French summary.]

I.J. Good & T.N. Tideman: Stirling Numbers and a Geometric Structure from Voting Theory, J. Combinatorial Theory A 23,1 (1977) 34-45

Henry W. Gould: A Note on the Number of Linearly Inducible Orderings of Points in d-Space, SIAM Journal on Applied Mathematics 26,3 (1974) 528-530.

Henry Gould & Jocelyn Quaintance: are supposedly writing a book about Stirling Number identities, which to be published by World Scientific in 2015. Their online file http://www.math.wvu.edu/~gould/Vol.7.PDF will be part of it.

Branko Grünbaum: Convex Polytopes, Wiley Interscience (Pure and Applied Mathematics #16), New York, 1967.

L.H. Harper: Stirling Behavior is Asymptotically Normal, Annals Math'l. Statist. 38,2 (1967) 410-414.

Manuel Kauers: Summation algorithms for Stirling number identities, J. Symbolic Computation 42,10 (2007) 948-970,

Charles Knessl & Joseph B. Keller: Stirling number asymptotics from recursion equations using the ray method, Studies in Appl. Math. 84 (1991) 43-56.

Vaclav Kotesovec: Interesting asymptotic formulas for binomial sums, manuscipt published on his web page, dated June 2013.

Elliott H. Lieb: Concavity properties and a generating function for Stirling numbers, J. Combinatorial Theory 5 (1968) 203-206. Shows both kinds of (unsigned) Stirling numbers are "strongly logarithmically concave" that is StirlingS2(N,K)²>StirlingS2(N,K-1)·StirlingS2(N,K+1) for 2≤K≤N-1. This implies both kinds of Stirling numbers are "unimodal," i.e. have a unique maximum (except perhaps it could be bi-unique, i.e. is co-equally maximized at two consecutive Ks) as a functions of K. Lieb did not realize it, but his result actually was a rediscovery of a remark published by J.M.Hammersley in 1951. Erdös 1953, following up on Hammersley, further showed the |StirlingS1| maximum is genuinely unique (and occurs at either K=1+⌊ln(N-1)⌋ or K=⌊ln(N-1)⌋ for all N≥198) for all N≥3. Indeed, all the StirlingS1(N,K) for a given N are distinct for each N>10⁸ and more strongly (which Erdös claimed without giving his proof) for each N≥5000. With computers it ought to be possible to examine all the cases below 5000 too, thus compeltely settling the problem.

Guy Louchard: Asymptotics of the Stirling numbers of the first kind revisited: A saddle point approach, Discrete Mathematics & Theoretical Computer Science 12,2 (2010) 167-184.

Joseph Malkevitch: Euler's Polyhedral Formula, introductory essay at Amer. Math. Society's web site.

Leo Moser & Max Wyman: Asymptotic development of the Stirling numbers of the first kind, J.London Math'l. Soc. 33 (1958) 133-146.

Leo Moser & Max Wyman: Stirling numbers of the second kind, Duke Math. J. 25,1 (1958) 29-43.

Albert Nijenhuis & Herbert S. Wilf: Combinatorial algorithms, Academic Press 2nd ed 1978.

NIST digital library of mathematical functions, §26.7 covers Bell numbers, §26.8 Stirling numbers, and §4.13 the LambertW function.

Peter Orlik & Hiroaki Terao: Arrangements of Hyperplanes, Grundlehren der mathematischen Wissenschaften 300, Springer-Verlag, Berlin/New York, 1992. QA167.O75.

L.A.Shepp & S.P.Lloyd: Ordered cycle lengths in a random permutation, Trans. Amer. Math. Soc. 121,2 (1966) 340-357.

Richard P. Stanley: An Introduction to Hyperplane Arrangements, 109 pages of notes published pp. 389-496 in Geometric Combinatorics (Ezra Miller, Victor Reiner, and Bernd Sturmfels, eds.), IAS/Park City Mathematics Series, vol. 13, American Mathematical Society, Providence, RI, 2007. Errata (pdf file, version of 28 January 2009, applying to the Park City published version; most of the errors found by Steven Sam). Library of congress catalog number QA167.G459.

Nico M. Temme: Asymptotic estimates of Stirling numbers, Stud. Appl. Math. 89,3 (1993) 233-243.

A.N. Timashev: On asymptotic expansions of Stirling numbers of the first and second kinds, Diskretnaya Matematika 10,3 (1998) 148-159 [in Russian] = Discrete Mathematics and Applications 8,5 (1998) 533-544 [English translation].

Horst Wegner: An Almost Accurate Location of the Maximum Stirling Number(s) of the Second Kind, Results in Maths 61, 3-4 (June 2012) 231-243.

Herbert S. Wilf: The asymptotic behavior of the Stirling numbers of the first kind (note), J. Combinatorial Theory A 64,12 (1993) 344-349.

Thomas Zaslavsky: Facing up to arrangements: face-count formulas for partitions of space by hyperplanes, Memoirs Amer. Math. Soc. 1,1 (1975) Number 154.

Thomas Zaslavsky: A combinatorial analysis of topological dissections, Advances in Maths. 25,3 (1977) 267-285. Also briefly summarized in Counting the faces of cut-up spaces, Bulletin Amer. Math. Soc. 81 (1975) 916-918.

Thomas Zaslavsky: Extremal arrangements of hyperplanes, pp. 69-87 in Discrete Geometry and Convexity (New York, 1982) = volume 440 of Annals New York Academy of Sciences 1985.

Thomas Zaslavsky: Perpendicular Dissections of Space, Discrete & Computational Geometry 27,3 (January 2002) 303-351.

Return to main page